前言
逻辑回归的一个小案例,使用sklearn自带的一个数据
代码
1
2
3
4
5
6
|
from sklearn.linear_model import LogisticRegression as LR #逻辑回归
from sklearn.datasets import load_breast_cancer #导入乳腺癌数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split # 导入分测试与训练集
from sklearn.metrics import accuracy_score#精确性分数
|
1
2
|
data = load_breast_cancer()#乳腺癌数据集
data
|
{'data': array([[1.799e+01, 1.038e+01, 1.228e+02, ..., 2.654e-01, 4.601e-01,
1.189e-01],
[2.057e+01, 1.777e+01, 1.329e+02, ..., 1.860e-01, 2.750e-01,
8.902e-02],
[1.969e+01, 2.125e+01, 1.300e+02, ..., 2.430e-01, 3.613e-01,
8.758e-02],
...,
[1.660e+01, 2.808e+01, 1.083e+02, ..., 1.418e-01, 2.218e-01,
7.820e-02],
[2.060e+01, 2.933e+01, 1.401e+02, ..., 2.650e-01, 4.087e-01,
1.240e-01],
[7.760e+00, 2.454e+01, 4.792e+01, ..., 0.000e+00, 2.871e-01,
7.039e-02]]),
'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0,
1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0,
1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1,
1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0,
0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1,
1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0,
1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1,
1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0,
0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0,
0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0,
1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1,
1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0,
1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1,
1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1,
1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1]),
'frame': None,
'target_names': array(['malignant', 'benign'], dtype='<U9'),
'DESCR': '.. _breast_cancer_dataset:\n\nBreast cancer wisconsin (diagnostic) dataset\n--------------------------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 569\n\n :Number of Attributes: 30 numeric, predictive attributes and the class\n\n :Attribute Information:\n - radius (mean of distances from center to points on the perimeter)\n - texture (standard deviation of gray-scale values)\n - perimeter\n - area\n - smoothness (local variation in radius lengths)\n - compactness (perimeter^2 / area - 1.0)\n - concavity (severity of concave portions of the contour)\n - concave points (number of concave portions of the contour)\n - symmetry\n - fractal dimension ("coastline approximation" - 1)\n\n The mean, standard error, and "worst" or largest (mean of the three\n worst/largest values) of these features were computed for each image,\n resulting in 30 features. For instance, field 0 is Mean Radius, field\n 10 is Radius SE, field 20 is Worst Radius.\n\n - class:\n - WDBC-Malignant\n - WDBC-Benign\n\n :Summary Statistics:\n\n ===================================== ====== ======\n Min Max\n ===================================== ====== ======\n radius (mean): 6.981 28.11\n texture (mean): 9.71 39.28\n perimeter (mean): 43.79 188.5\n area (mean): 143.5 2501.0\n smoothness (mean): 0.053 0.163\n compactness (mean): 0.019 0.345\n concavity (mean): 0.0 0.427\n concave points (mean): 0.0 0.201\n symmetry (mean): 0.106 0.304\n fractal dimension (mean): 0.05 0.097\n radius (standard error): 0.112 2.873\n texture (standard error): 0.36 4.885\n perimeter (standard error): 0.757 21.98\n area (standard error): 6.802 542.2\n smoothness (standard error): 0.002 0.031\n compactness (standard error): 0.002 0.135\n concavity (standard error): 0.0 0.396\n concave points (standard error): 0.0 0.053\n symmetry (standard error): 0.008 0.079\n fractal dimension (standard error): 0.001 0.03\n radius (worst): 7.93 36.04\n texture (worst): 12.02 49.54\n perimeter (worst): 50.41 251.2\n area (worst): 185.2 4254.0\n smoothness (worst): 0.071 0.223\n compactness (worst): 0.027 1.058\n concavity (worst): 0.0 1.252\n concave points (worst): 0.0 0.291\n symmetry (worst): 0.156 0.664\n fractal dimension (worst): 0.055 0.208\n ===================================== ====== ======\n\n :Missing Attribute Values: None\n\n :Class Distribution: 212 - Malignant, 357 - Benign\n\n :Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian\n\n :Donor: Nick Street\n\n :Date: November, 1995\n\nThis is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.\nhttps://goo.gl/U2Uwz2\n\nFeatures are computed from a digitized image of a fine needle\naspirate (FNA) of a breast mass. They describe\ncharacteristics of the cell nuclei present in the image.\n\nSeparating plane described above was obtained using\nMultisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree\nConstruction Via Linear Programming." Proceedings of the 4th\nMidwest Artificial Intelligence and Cognitive Science Society,\npp. 97-101, 1992], a classification method which uses linear\nprogramming to construct a decision tree. Relevant features\nwere selected using an exhaustive search in the space of 1-4\nfeatures and 1-3 separating planes.\n\nThe actual linear program used to obtain the separating plane\nin the 3-dimensional space is that described in:\n[K. P. Bennett and O. L. Mangasarian: "Robust Linear\nProgramming Discrimination of Two Linearly Inseparable Sets",\nOptimization Methods and Software 1, 1992, 23-34].\n\nThis database is also available through the UW CS ftp server:\n\nftp ftp.cs.wisc.edu\ncd math-prog/cpo-dataset/machine-learn/WDBC/\n\n.. topic:: References\n\n - W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction \n for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on \n Electronic Imaging: Science and Technology, volume 1905, pages 861-870,\n San Jose, CA, 1993.\n - O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and \n prognosis via linear programming. Operations Research, 43(4), pages 570-577, \n July-August 1995.\n - W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques\n to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994) \n 163-171.',
'feature_names': array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error',
'fractal dimension error', 'worst radius', 'worst texture',
'worst perimeter', 'worst area', 'worst smoothness',
'worst compactness', 'worst concavity', 'worst concave points',
'worst symmetry', 'worst fractal dimension'], dtype='<U23'),
'filename': '/home/ubuntu/.local/lib/python3.8/site-packages/sklearn/datasets/data/breast_cancer.csv'}
1
2
|
X = data.data
X.shape
|
(569, 30)
1
2
|
y = data.target
y.shape
|
(569,)
(569, 30)
1
2
|
lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)#l1 正则化会压缩到0
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)#l2 正则化不会压缩到0,默认l2正则化不填的话
|
1
2
3
|
#逻辑回归的重要属性coef_,查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_
|
array([[ 4.00409758, 0.03192262, -0.13763277, -0.01622177, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.50529191, 0. , -0.07128513, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , -0.2458918 , -0.12855748, -0.01441275, 0. ,
0. , -2.03953157, 0. , 0. , 0. ]])
1
|
(lrl1.coef_ != 0).sum(axis=1)#array([10]) 30个特征中有10个特征的系数不为0
|
array([10])
1
2
|
lrl2 = lrl2.fit(X,y)
lrl2.coef_
|
array([[ 1.61331113e+00, 1.00124606e-01, 4.60084835e-02,
-4.19839426e-03, -9.26228937e-02, -3.00484301e-01,
-4.53250190e-01, -2.19778015e-01, -1.33074668e-01,
-1.92576286e-02, 1.89635811e-02, 8.74998561e-01,
1.32421950e-01, -9.53784315e-02, -9.62972408e-03,
-2.53596204e-02, -5.83890299e-02, -2.67755115e-02,
-2.73846616e-02, -8.05302922e-05, 1.28529688e+00,
-3.00088054e-01, -1.74310770e-01, -2.23545072e-02,
-1.70267493e-01, -8.77272211e-01, -1.15830085e+00,
-4.22526360e-01, -4.12406225e-01, -8.66393364e-02]])
array([[ True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1.5,19):
lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
lrl1 = lrl1.fit(Xtrain,Ytrain)
l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):
plt.plot(np.linspace(0.05,1.5,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示,右下角
plt.show()#0.8~0.9比较好
|

1
2
3
4
5
6
|
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel
|
1
2
|
data = load_breast_cancer()
data.data.shape
|
(569, 30)
1
2
|
LR_ = LR(solver="liblinear",C=0.9,random_state=420)
cross_val_score(LR_,data.data,data.target,cv=10).mean()
|
0.9508145363408522
1
2
3
|
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
#threshold=float筛选特征的一个阈值,norm_order范式为l1,嵌入法
X_embedded.shape
|
(569, 9)
1
|
cross_val_score(LR_,X_embedded,data.target,cv=10).mean()#0.9368323826808401
|
0.9368107769423559
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
fullx = []
fsx = []
threshold = np.linspace(0,abs((LR_.fit(data.data,data.target).coef_)).max(),20)
k=0
for i in threshold:
X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(data.data,data.target)
fullx.append(cross_val_score(LR_,data.data,data.target,cv=5).mean())
fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=5).mean())
print((threshold[k],X_embedded.shape[1]))
k+=1
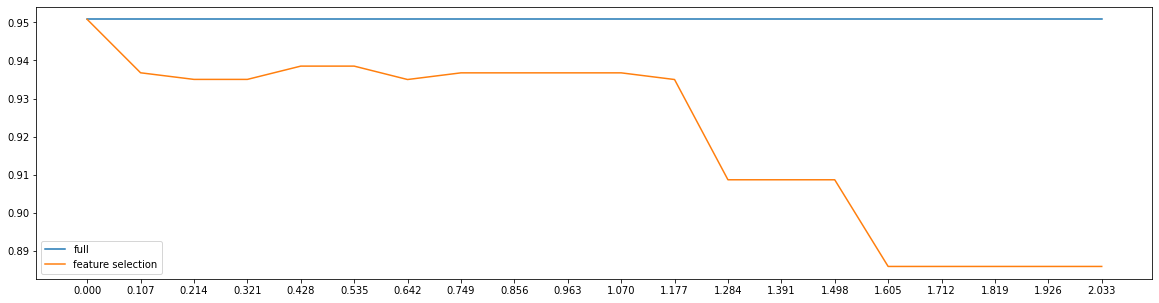
plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label="full")
plt.plot(threshold,fsx,label="feature selection")
plt.xticks(threshold)
plt.legend()
plt.show()
|
(0.0, 30)
(0.10700725930906944, 17)
(0.2140145186181389, 12)
(0.3210217779272083, 11)
(0.4280290372362778, 8)
(0.5350362965453472, 8)
(0.6420435558544166, 6)
(0.7490508151634862, 5)
(0.8560580744725556, 5)
(0.963065333781625, 5)
(1.0700725930906945, 5)
(1.1770798523997639, 4)
(1.2840871117088333, 2)
(1.3910943710179027, 2)
(1.4981016303269723, 2)
(1.6051088896360417, 1)
(1.712116148945111, 1)
(1.8191234082541805, 1)
(1.92613066756325, 1)
(2.0331379268723193, 1)